KNN原理详解郝伟 2021/10/07 [TOC]

1. 1 简介

在机器学习中，有大量的分类算法，如线性回归，逻辑回归，K邻近算法等。本文将对K近邻法算法进行详细介绍。 K近邻(k-nearest neighbors, KNN)，是一种常用回归算法，学用于机器分类，是机器学习算法中最基础、最简单的算法之一， 1968年由 Cover和 Hart 提出，应用场景有字符识别、文本分类、图像识别等领域。用于对样本的类别进行智能区分，在各个领域都有有广泛的应用。比如，判断一个人的性别，只需要根据身体、体重、三围，就可以进行分类判断。

2. 2 核心思想

KNN的核心思路包括三步根据样本的n个特征建立n维度的向量空间，再根据样本的分布，将样本分成N类，然后根据分布空间，预测新的样本。

2.1. 2.1 基本计算步骤

主要分为以下三步： 1）定义n个特征； 2）将样本用已定义的n维向量表示; 3）定义距离K使得所有样本空间会分为若干个子空间，在空间内的样本距离都小于K。

其中，需要注意一点，KNN的一些实现算法中，K值的确定不是简单的直线距离，可能是比较复杂的计算方法，以满足不同的需求。通过样本集的学习，可以得到若干个子空间的定义，再根据这个定义对新数据进行预测。

2.2. 2.2 主要因素

KNN的实现主要需要考虑以下三个因素：

距离度量的方法，即如何对两个n维的距离进行测量；
K值的选取，根据距离试题方法确定K值选定；
子空间分类表示方法，即确定如何确定子空间的表示方法。

最后，需要注意KNN是监督学习，所以每个样本不仅需要每个特征的数据，还需要对分类结果进行标记。

2.3. 2.3 主要特性

优点
- 算法本身简单、易于理解和实现
- 精度较高、对异常值不敏感
- 适用于大样本自动分类
- 需要参数估计很少，只有一个邻居个数 k kk
- 惰性学习，学习阶段仅仅是保存数据而已
缺点
- 计算时间复杂度高
- 内存开销大，训练数据停驻在内存中
- 输出可解释性不强

3. 3 距离计算公式

常见的点距离估计公式有很多种，如欧式距离公式、曼哈顿距离公式、闵可夫斯基距离公式、切比雪夫距离、余弦公式等，本文主要介绍前三种。

3.1. 3.1 欧式距离公式

距离的度量方式有很多，最为常用的是欧式距离，对于两个 n 维变量 $\textbf{x}(x_1,x_2,...,x_n)$ 和 $\textbf{y}(y_1,y_2...,y_n)$，根据欧式距离公式有： $- \to xy = | | y - x | | = \sqrt{(y_{1} - x_{1})^{2} + (y_{2} - x_{2})^{2} + . . . + (y_{n} - x_{n})^{2}} = \sqrt{n \sum i = 1 (y_{i} - x_{i})^{2}}$

当$\textbf{x}$为原点$\textbf{o}$时，$\textbf{y}$到$\textbf{x}$的距离就是$\textbf{y}$到原点$\textbf{o}$的距离，即： $- \to oy = | | y | | = \sqrt{y_{1}^{2} + y_{2}^{2} + . . . + y_{n}^{2}} = n \sum i = 1 y_{i}^{2}$

3.2. 3.2 曼哈顿距离公式

除了欧式距离公式，还有曼哈顿距离公式：

$- \to xy = | | y - x | | = | y_{1} - x_{1} | + | y_{2} - x_{2} | + . . . + | y_{n} - x_{n}) | = n \sum i = 1 | y_{i} - x_{i} |$

3.3. 3.3 闵可夫斯基距离公式

闵可夫斯基距离(Minkowski Distance)公式定义如下： $- \to xy = | | y - x | | = \sqrt[p]{(y_{1} - x_{1})^{p} + (y_{2} - x_{2})^{p} + . . . + (y_{n} - x_{n})^{p}} = \sqrt[p]{n \sum i = 1 (y_{i} - x_{i})^{p}}$

显然易见，闵可夫斯基距离公式是以上两种公式的统一，分别是p=1和p=2的特殊情况。

4. 4. K值的选择和影响

K是K近邻算法中需要确定的一个重要参数，也是一个超参数。

注：机器学习中的超参数是在学习过程前就需要确定其值的参数。

在KNN中，一般通过对样本的分析，可以对K进行初步确定，然后再经过多次迭代优化，提高学习的性能。如果K值设置不合理，则会有以下问题：

K值偏小，会导致预测模型对近邻点的周围的点相对敏感，易受到噪声点的干扰，从而导致过拟合；
K值偏大，预测模型鲁棒性会比较好，可以减少的估计误差，但对数据敏感度下降，易导致欠拟合。

5. 5. 决策函数的选择

5.1. 5.1 用于分类的多票表决法

在分类任务中可使用投票法，即选择这k个实例中出现最多的标记类别作为预测结果。

5.2. 5.2 用于回归的平均值法

另外，KNN算法不仅用于分类，也可用于回归 —— 回归与分类的根本区别在于输出空间是否为一个度量空间。所以，如果数据向量的对应的标签（类别）也可以进行量化衡量的话，那么采用平均值法或加权平均值法就可以得出测试点的预测值。

6. 6. Scikit-Learn中的实现

在Scikit-Learn中使用了蛮力法(Brute-Force)，KD树(KDTree)和球树(BallTree)三种实现，具体参见[3, 4]。

7. 7. 其他

在n维的样本空间$\textbf{D}$=${\textbf{x}_1, \textbf{x}_2,...,\textbf{x}_m}$中，第$j$个特征向量的可以表示为： $x_{j} = (x_{j}^{1}, x_{j}^{2}, . . ., x_{j}^{n})^{T}$

无监督样本空间 $\textbf{D}$=${\textbf{x}_1, \textbf{x}_2,...,\textbf{x}_m}$ 有监督样本空间 $\textbf{D}$=${(\textbf{x}_1, y_1), (\textbf{x}_2, y_2),...,(\textbf{x}_m, y_m)}$

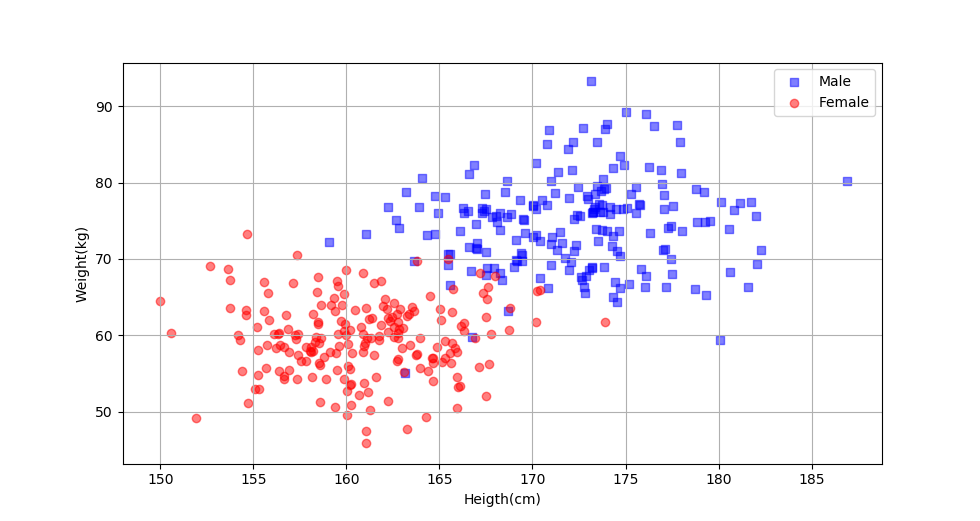
8. 附：男女性别划分示例

9. 参考资料

[1] K近邻法(KNN)原理小结, https://www.cnblogs.com/pinard/p/6061661.html [2] 机器学习入门 —— 超级详细的KNN算法学习笔记, https://blog.csdn.net/qq_44846324/article/details/114270003 [3] scikit-learn K近邻法类库使用小结, https://www.cnblogs.com/pinard/p/6065607.html [4] Official API Documentation, https://scikit-learn.org/stable/modules/generated/sklearn.datasets.make_classification.html [5] 机器学习的基本术语理解, https://zhuanlan.zhihu.com/p/92912335

KNN原理详解 2021/10/07