使用numpy进行连续函数的线性拟合郝伟 2021/07/07 [TOC]

1. 简介

线性拟合是回归问题的重要内容，本文将通过一个实例了解一下numpy的线性拟合的用法。

2. 基本知识

多式项拟合是经常用到的一种通过多个离散点推导出原函数的过程。数学描述如下：设函数 $y = a_{1} x_{1} + a_{2} x_{2} + . . . + a_{n} x_{n}$

其中系数为 $A$ = $[a_1$, $a_2$, ..., $a_n]$， $n$ 的值表示函数的阶数。

在实际应用中，如果函数$A$和$x$已知，我们很容易求出 y 的值。但是在在实际应用中，可能是有m个离散点的集合 ${(x_1, y_1), (x_2, y_2),..., (x_m, y_m)}$，然后根据这些离散点的信息，求出 $A$。比如，我们已经知道近10年淘宝的销售额，那么能否找到若干个系数 $A$ 来定义一个多项式函数进行表示。

3. 实现技术

为了实现这个需求，在本算法中使用了以下两个核心功能函数：

np.polyfit(xs, ys, degree)（官方说明文档），对序列 xs 和 ys 按 deg 阶进行拟合，返回序列$A$，其中：
- xs 为X轴的值；
- ys 为Y轴的值；
- degree 表示阶数(the degree of the polynomial), 见下文。
np.poly1d(coefficients) （官方说明文档）用于生成一维的函数，其中:
- coefficients 表示系数$A$，即则 np.polyfit(xs, ys, degree) 生成。

4. 演示代码

本代码的核心内容是使用多项式进行拟合。代码中对1至5阶的多项式进行拟合，然后计算不同阶的残差并输出。

# encoding=utf-8
'''
作者：郝伟老师
日期：2021/07/06
描述：用于验证连续函数的拟合问题。
历史：
'''

import numpy as np
import matplotlib.pyplot as plt


# 表示 2009 - 2018这十年
years = np.arange(2009, 2019, 1)

# 淘宝2009-2018的实际数据，网上可查。
sales = np.array([0.52, 9.36, 33.60, 191.00, 362.00, 571.00, 912.00, 1207.00, 1682.00, 2135.00]) 

res = []
for i in range(5):
    # 多项式阶数
    degree = i + 1
    print(' {}阶拟合 '.format(degree).center(60, '*'))

    # 三次多项式拟合，计算coefficients的值
    coefficients = np.polyfit(years, sales, degree)

    # 利用计算的系数值，生成这个多式项函数f
    predic_fun = np.poly1d(coefficients) 

    # 计算残差（越小越好）
    predicted_sales=predic_fun(years)
    residual=sales-predicted_sales
    print('方差：{0:8.3f}'.format(residual.var()))

    # predic_fun(2019) 预测2019年的数据。
    print('淘宝{0}年的数据预计为：{1:8.3f}亿元。'.format(2019, predic_fun(2019)))

    res.append((degree, residual.var(), predic_fun(2019)))

    plt.plot(years, predicted_sales)

# 所有结果对比
print(' 结果对比 '.center(60, '*'))
for item in res:
    print('{0}\t{1:8.3f}\t{2:8.3f}'.format(item[0], item[1], item[2]))

plt.show()

5. 输出

*************************** 1阶拟合 ***************************
方差：47831.748
淘宝2019年的数据预计为：2015.608亿元。
*************************** 2阶拟合 ***************************
方差： 380.843
淘宝2019年的数据预计为：2675.128亿元。
*************************** 3阶拟合 ***************************
方差： 379.772
淘宝2019年的数据预计为：2680.181亿元。
*************************** 4阶拟合 ***************************
方差： 377.720
淘宝2019年的数据预计为：2692.278亿元。
*************************** 5阶拟合 ***************************
sys:1: degreeWarning: Polyfit may be poorly conditioned
方差： 377.723
淘宝2019年的数据预计为：2692.282亿元。
*************************** 结果对比 ***************************
1       47831.748       2015.608
2        380.843        2675.128
3        379.772        2680.181
4        377.720        2692.278
5        377.723        2692.282

注意，当degree=5时，出现了sys:1: degreeWarning: Polyfit may be poorly conditioned的提示，这里的意思

6. 图像

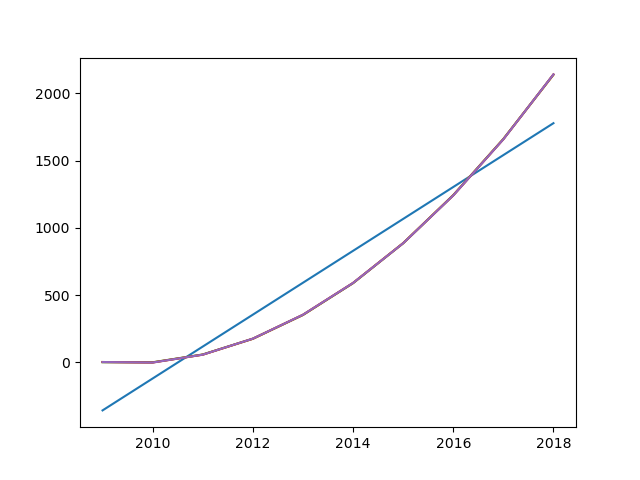
如图所示，可以发现除了1阶差的比较大，在本示例中其他阶相差不多（这点从上面的输出也可以看出来）。

使用numpy进行连续函数的线性拟合 2021/07/07