深入理解人工智能模型能力指标F1的具体意义 郝伟 2021/05/14 [TOC]
1. 简介
在对人工智能训练能力水平评估的标准中，准确性（Accuracy），精准度（Precision），召回率（Recall）和 综合指标 F1。 三前者相对比较好理解，基具体定义如下：
- 准确率（ACC）：(TP+TN)/(TP+FP+TN+FN)
- 精准率（PRE）：TP / (TP + FN)
- 召回率（REC）：TP / (TP + TN)
但是F1的定义相对复杂一些，定义如下： F1的含意很少有人能说清楚。为了深入理解F1的本质，本文通过一个具体实例，解读F1的含意。
2. 示例
首先，让我们来考虑这样一个情况，你去公司上班，坐公交车去的，回来打的。假设距离是5公里，坐公交用时30分钟。回来时打的，用时15分钟。那么应该如何计算往返的平均速度呢？
- 公交速度：5km / 0.5h = 10 km/h
- 打的速度：5km / 0.25h = 20 km/h
那么我们可以计算出两个速度：
- 算术平均速度：$(10 + 20)/2 = 15$ km/h
- 调和平均速度：$10 / (0.5+0.25) = 13.33$ km/h
通过简单地将5约去，我们就得到了调和公式：
从这里可以看出，调整平均数更能够真实地反应平均速度，平均速度表达不够合理。根本原则在于作用的时间不同。在本示例上，公交车做了30分钟，而打的只有15分钟，所以在计算平均速度的时候，如果只是单纯地累加除以二，显然无法体现出这一点。而调和平均值却可以。同时，调和平均值也解释了为什么值不能取0：当速度为0时，那么永远无法达到终点，所以平均速度就没有意义。
另外再看下调整平均数的变化速度，其中 x = [0.01, 0.02, ..., 1.0], y = [0.01, 0.02, ..., 1.0]， $z=F1$。
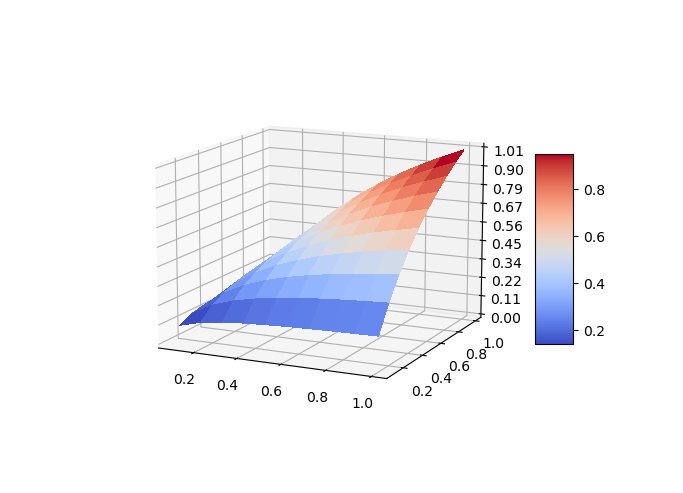根据图像显示，在不同的两百分比值（0-1之间）x,y的变化情况下，可以发现，只有当两者都大时，F1才会比较大，只有一个大，另一个小时，则会偏小。仍然以上面的速度举例来说，无论是出发用还是返回，如果速度过慢导致用时过多，都会造成整体用时明显过多，从而导致总速度有过慢。比如，出发用时正常的10分钟，但是返回时遇到大堵车，用时5小时，那么总速度就会受到堵车的显著影响，所体现出来的总速度中返回速度起到主导因素，而出发用时可以忽略不计。所以，如果想得到较高的F1，必需两个速率都高才可以，如果一个过低，则会拖累F1过低，即F1体现的整体性能，必需不能有短板，才能达到较高的F1。反观算术平均值，那么就无法体现出这点，就会出现一个普通人和马云一平均，普通人也变成亿万富翁的假象。
最后，顺便提下，几何平均速度为 $\sqrt{10*20} = 17.32$ km/h
3. 结论
调和平均数是用于计算速率的平均值，比如在F1中，是求精准率和召回率的指标。通过对再者求调和平均数，能够更好地反应两者的实际平均情况。
4. 附：调和曲线绘制函数
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.ticker import LinearLocator
space = np.linspace(0.01, 1, num=100)
#data = np.zeros((100,100), dtype=float)
data = []
for ri in range(100):
row = [0] * 100
for ci in range(100):
x = 0.01 * ri + 0.01
y = 0.01 * ci + 0.01
row[ci] = 2 * x * y / ( x + y)
data.append(row)
#plt.plot(data)
np.random.seed(19680801)
z = np.random.rand(6, 10)
x = np.arange(-0.5, 10, 1) # len = 11
y = np.arange(4.5, 11, 1) # len = 7
#fig, ax = plt.subplots()
#ax.pcolormesh(x, y, Z)
x = np.linspace(0.1, 1, num=10)
y = np.linspace(0.1, 1, num=10)
x, y = np.meshgrid(x, y)
z = 2 * x * y / (x + y)
#z = np.zeros((10, 10), dtype=float)
plt.pcolormesh(x, y, z)
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
# Plot the surface.
surf = ax.plot_surface(x, y, z, cmap=cm.coolwarm,
linewidth=0, antialiased=False)
# Customize the z axis.
ax.set_zlim(0, 1.01)
ax.zaxis.set_major_locator(LinearLocator(10))
# A StrMethodFormatter is used automatically
ax.zaxis.set_major_formatter('{x:.02f}')
# Add a color bar which maps values to colors.
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.show()