梯度下降计实例计算(三维) 郝伟 2021/03/09 [TOC]

1. 函数定义

已经函数 $z=f(x, y) = (x-4)^2 + (y - 4)^2=x^2+y^2-8x-8y+32$。方向导数分别为

• $z$的$x$偏导数: $\frac{\partial z}{\partial x} = 2x-8$
• $z$的$y$偏导数: $\frac{\partial z}{\partial x} = 2y-8$

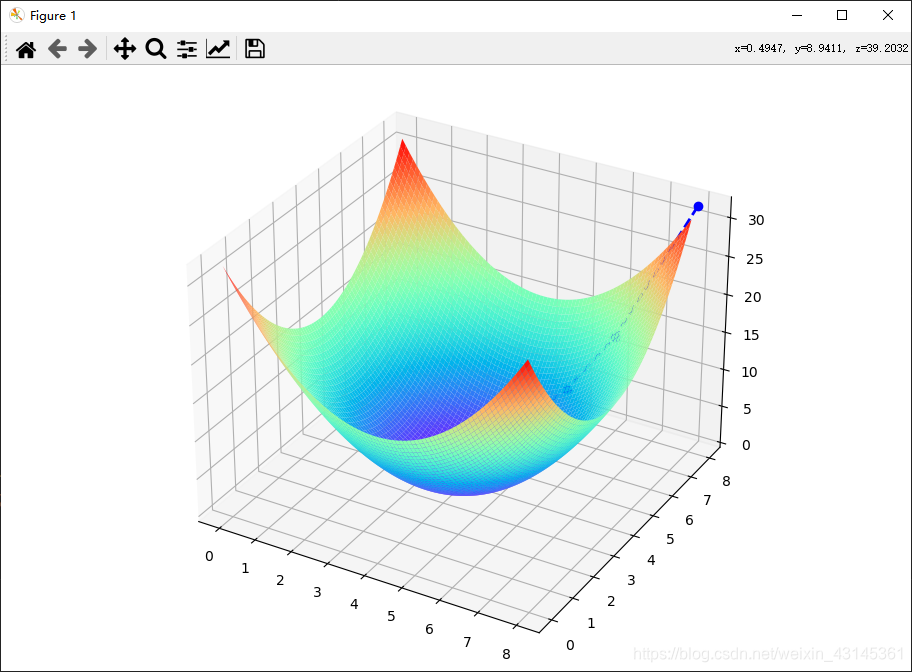
从点 (0,0) 开始迭代，步长为0.2，可以得到以下内容。

#encoding=utf-8
"""
创建日期：Sun Feb 21 16:19:17 2021
作者信息：郝伟老师
功能简介：
"""

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

def loss(x, y):
    return (x-4)**2 + (y - 4) ** 2

def g(t):
    return 2*t - 8

# 初始化值为x0, 学习率为0.9
x0, y0, rate=8, 8, 0.2

# 初始化 x和y
x, y, z=x0, y0, loss(x0, y0)

# 记录中间的过程值
xs, ys, zs=[], [], []
xs.append(x)
ys.append(y)
zs.append(z)

# 循环次数限制在100，保证不会因为递减缓慢而卡死
print('i       x               y               z        delta_z')
for i in range(100):
    # 核心代码，根据 g(x)的变化率以r的速度递减
    x = x - rate * g(x)
    y = y - rate * g(x)
    z_new=loss(x, y)
    offset_z = abs(z_new - z)
    print('{0}\t{1:.5e}\t{2:.5e}\t{3:.5e}\t{4:.5e}'.format(i+1, x, y, z, offset_z))
    if offset_z < 1e-6:
        print('i = ', i)
        break
    z = z_new
    xs.append(x)
    ys.append(y)
    zs.append(z)

# 绘制递减曲线
#%config InlineBackend.figure_formats = ['retina', 'svg']
fig=plt.figure()
ax=Axes3D(fig)
xs2=np.arange(0, 8, .1)
ys2=np.arange(0, 8, .1)
xs2, ys2 = np.meshgrid(xs2, ys2)
zs2 = (xs2-4)**2 + (ys2 - 4) ** 2
ax.plot_surface(xs2, ys2, zs2, rstride=1, cstride=1, cmap='rainbow')
ax.set_title('GD solution: x=%.2f, y=%.2f, z=%.2f' % (x, y, z))
plt.plot(xs, ys, zs, 'bo--', linewidth=2)
plt.show()

--- END ---