梯度下降计实例计算(二维) 郝伟 2021/02/22 [TOC]
1. 内容简介
梯度下降是在机器学习中重要的计算内容。本文就一个具体的示例,展示如何在梯度下降中。
2. 示例说明
设损失函数 $y=loss(x)=(x-4)^2$,令此函数的导数为$g(x)=y'=loss'(x)=2x-8$。 在一般情况下,如果可以得到$g(x)$,那么只要解出 $g(x)=0$的根,那么就求得了最小值。比如在本示例中,很容易得到在$x=0$时,取得最小值。
但是在实际的情况下,问题往往不是那么简单,即使有了 $loss(x)$ 和 $g(x)$,但是方程 $g(x)=0$,难以解出,那么就有了梯度下降法:
为了理解这个公式,首先我们需要理解一下导数的基本概念。给定函数 $y=f(x)$,则其导数的定义如下:
由公式可见,对点$x0$的导数的几何含义是函数在点$x0$处的变化速率或斜率。当变量增加时,(即多维函数),斜率不再是一维的,于是就有了梯度的概念。梯度是一个向量组合,其几何含义是多维图形中变化速率最快的方向。
有了这个概念再看公式1,可以发现通过r,能够根据y的变化率进行推进,从而逐渐逼近最小值的点。具体过程如下代码所示:
#encoding=utf-8
"""
创建日期:Sun Feb 21 16:19:17 2021
作者信息:郝伟老师
功能简介:
"""
import matplotlib.pyplot as plt
import numpy as np
def loss(x):
return (x-4)**2
def g(x):
return 2*x - 8
# 初始化值为x0, 学习率为0.9
x0, rate=0, 0.1
# 初始化 x和y
x, y=x0, loss(x0)
# 记录中间的过程值
xs, ys=[], []
xs.append(x)
ys.append(y)
# 循环次数限制在100,保证不会因为递减缓慢而卡死
print('i x y delta_y')
for i in range(100):
# 核心代码,根据 g(x)的变化率以r的速度递减
x = x - rate * g(x)
y_new=loss(x)
print('{0}\t{1:.5e}\t{2:.5e}\t{3:.5e}'.format(i+1, x, y, abs(y_new-y)))
if abs(y_new - y) < 1e-6:
break
y = y_new
xs.append(x)
ys.append(y)
# 绘制递减曲线
plt.plot(xs, ys, 'bo--')
# 绘制函数 y=loss(x),其中 x in [0, 8]
xs2=np.arange(0.0, 8.0, 0.1)
ys2=[loss(x) for x in xs2]
plt.plot(xs2, ys2, '-', linewidth=2)
plt.show()
3. 绘制曲线
程序运行以后,可以得到以下曲线。
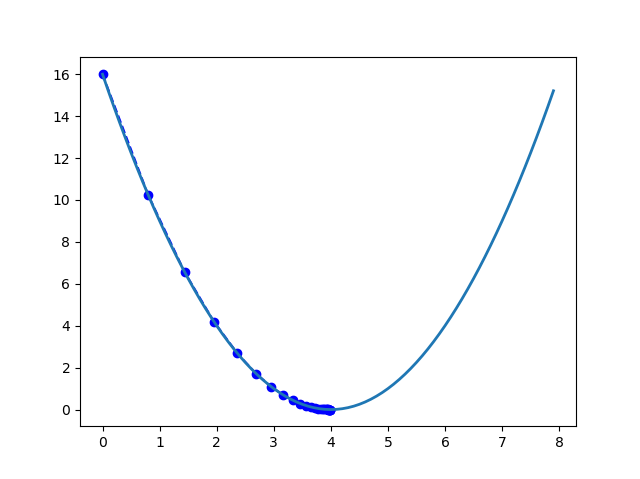
过程数据
i x y delta_y
1 8.00000e-01 1.60000e+01 5.76000e+00
2 1.44000e+00 1.02400e+01 3.68640e+00
3 1.95200e+00 6.55360e+00 2.35930e+00
4 2.36160e+00 4.19430e+00 1.50995e+00
5 2.68928e+00 2.68435e+00 9.66368e-01
6 2.95142e+00 1.71799e+00 6.18475e-01
7 3.16114e+00 1.09951e+00 3.95824e-01
8 3.32891e+00 7.03687e-01 2.53327e-01
9 3.46313e+00 4.50360e-01 1.62130e-01
10 3.57050e+00 2.88230e-01 1.03763e-01
11 3.65640e+00 1.84467e-01 6.64083e-02
12 3.72512e+00 1.18059e-01 4.25013e-02
13 3.78010e+00 7.55579e-02 2.72008e-02
14 3.82408e+00 4.83570e-02 1.74085e-02
15 3.85926e+00 3.09485e-02 1.11415e-02
16 3.88741e+00 1.98070e-02 7.13053e-03
17 3.90993e+00 1.26765e-02 4.56354e-03
18 3.92794e+00 8.11296e-03 2.92067e-03
19 3.94235e+00 5.19230e-03 1.86923e-03
20 3.95388e+00 3.32307e-03 1.19631e-03
21 3.96311e+00 2.12676e-03 7.65635e-04
22 3.97049e+00 1.36113e-03 4.90007e-04
23 3.97639e+00 8.71123e-04 3.13604e-04
24 3.98111e+00 5.57519e-04 2.00707e-04
25 3.98489e+00 3.56812e-04 1.28452e-04
26 3.98791e+00 2.28360e-04 8.22095e-05
4. 进一步讨论
如果,我们选择比较大的步长,比如0.9,那么会导致步长过长,“跨”过最小值,同样可以收敛,得到以下图像。
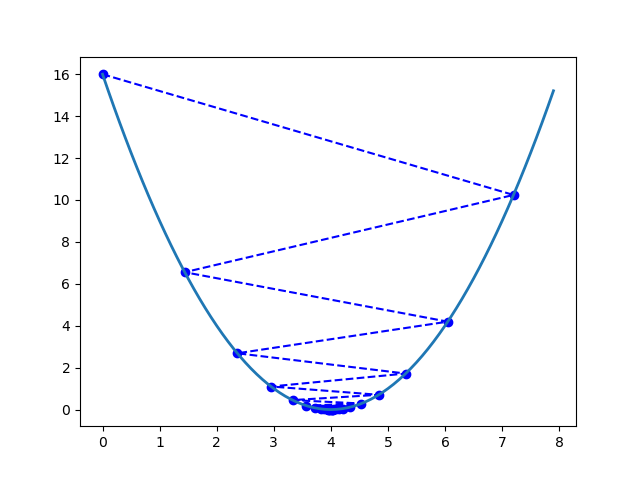
过程数据
i x y delta_y
1 7.20000e+00 1.60000e+01 5.76000e+00
2 1.44000e+00 1.02400e+01 3.68640e+00
3 6.04800e+00 6.55360e+00 2.35930e+00
4 2.36160e+00 4.19430e+00 1.50995e+00
5 5.31072e+00 2.68435e+00 9.66368e-01
6 2.95142e+00 1.71799e+00 6.18475e-01
7 4.83886e+00 1.09951e+00 3.95824e-01
8 3.32891e+00 7.03687e-01 2.53327e-01
9 4.53687e+00 4.50360e-01 1.62130e-01
10 3.57050e+00 2.88230e-01 1.03763e-01
11 4.34360e+00 1.84467e-01 6.64083e-02
12 3.72512e+00 1.18059e-01 4.25013e-02
13 4.21990e+00 7.55579e-02 2.72008e-02
14 3.82408e+00 4.83570e-02 1.74085e-02
15 4.14074e+00 3.09485e-02 1.11415e-02
16 3.88741e+00 1.98070e-02 7.13053e-03
17 4.09007e+00 1.26765e-02 4.56354e-03
18 3.92794e+00 8.11296e-03 2.92067e-03
19 4.05765e+00 5.19230e-03 1.86923e-03
20 3.95388e+00 3.32307e-03 1.19631e-03
21 4.03689e+00 2.12676e-03 7.65635e-04
22 3.97049e+00 1.36113e-03 4.90007e-04
23 4.02361e+00 8.71123e-04 3.13604e-04
24 3.98111e+00 5.57519e-04 2.00707e-04
25 4.01511e+00 3.56812e-04 1.28452e-04
26 3.98791e+00 2.28360e-04 8.22095e-05
5. 参考资料
[1] (二)深入梯度下降(Gradient Descent)算法,https://www.cnblogs.com/ooon/p/4947688.html