方向导数 郝伟 2020/01/15 [TOC]

1. 方向导数

在一维空间的变化率就是 $\frac{dx}{dy}$，也就是 $f'(x)$。在二维空间中，同样有导数，梯度是二维空间的导数，是某一点的变化情况。一维空间的导数只有大小，而二维空间有 $x,y$两个维度，所以在二维平面上就会形成一个方向。函数 $z = f(x, y)$ 在点 $(x_0, y_0)$的方向导数表示为： $\frac{\partial f}{\partial l}=\frac{\partial f}{\partial x}\overrightarrow{i}+\frac{\partial f}{\partial y}\overrightarrow{j}$

2. 梯度

函数 $z = f(x, y)$ 在点 $(x_0, y_0)$的梯度表示为： $\nabla f(x_0,y_0)=\sqrt{(\frac{\partial f}{\partial x}{)}^2+(\frac{\partial f}{\partial y}{)}^2}$

3. 示例

举例来说，设函数$y=f(x,y) =e^{-x^2 - y^2}$，其在点 $P(x_0, y_0)$ 方向导数可以表示如下： $$\frac{\partial f}{\partial l}=-2x_0{e}^{-x_0^2-y_0^2}\overrightarrow{i}-2y_0{e}^{-x_0^2-y_0^2}\overrightarrow{j}$$

其中 $\overrightarrow{i}$ 方向的系数由 $f$ 对 $x$ 的偏导数决定。类似的，$\overrightarrow{j}$ 方向的系数由 $f$ 对 $y$ 的偏导数决定。这样我们就可以求得点P在任意方向上的方向导数。其几何含义就是 $f$ 在点P所有方向的变化速率。

4. 几何意义

梯度的几何意义如如下图所示。 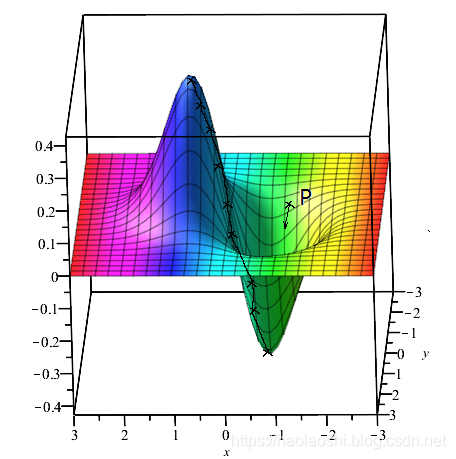比如，当$x=0, y=0$ 时，其方向导数为 $0\overrightarrow{j}+0\overrightarrow{j}$；而当 $x=1,y=1$ 时，$-2e^{-2}\overrightarrow{j}+-2e^{-2}\overrightarrow{j}$。

当曲面不是平面的时候，每个方向上的变化率是不一样的。如下图所示，在点P，其梯度就是在各个方向的变化。

再看另外的一个示例[2,3]，在这个示例中，如果要到达两个最低点（如下图所示），可以有两条不同的路径。这两条路径是最短路径，条件就是路径上的每点都是方向导数最小的点。

另外，发现Wikipedia上用来说明梯度的图片特别典型，说明非常形象，所以引来供大家学习。 设函数 $f(x, y) = -(cos2x + cos 2 y )^2$，则 $\nabla f$ 可以描述为在底部平面上的矢量投影，如下图所示。 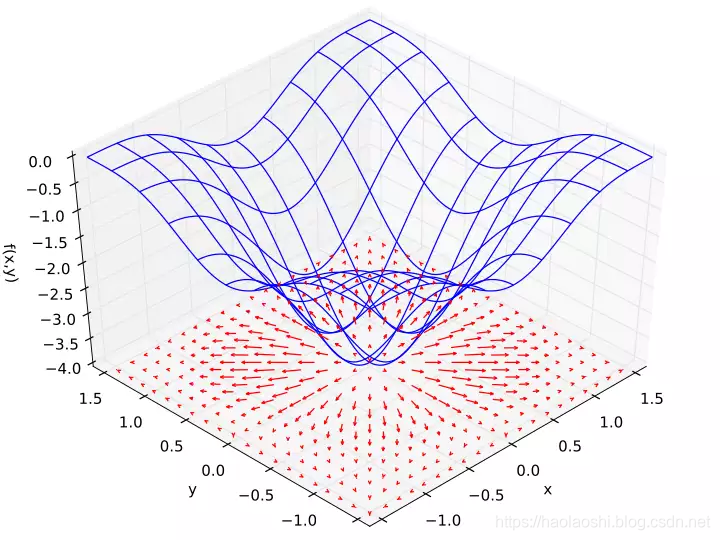根据图片所示，每个点的梯度是一个矢量，其长度代表了这点的变化速度，而方向表示了其变化速率最快的方向。所以通过这张图，我们可以很清楚地看到。在矢量长的地方，$f$ 的变化就明显，而其方向代表了增长最快的方向。 结合方向导数，我们可以很容易理解梯度其实就是指明函数在指定点的变量率最快的方向和大小。

5. 参考文献

[1] 西安建筑科技大学、第七节 方向导数与梯度，http://netedu.xauat.edu.cn/jpkc/netedu/jpkc/gdsx/homepage/5jxsd/51/513/5308/530807.htm [2] Pablo J. Villacorta，Introduction to Deep Learning Part 1: Neural Networks，https://www.stratio.com/blog/deep-learning-neural-networks-1，2017/09. [3] 没名字的蓝猫，深度解读机器学习“梯度下降”，https://www.jianshu.com/p/17191c57d7e9，2018/02.