残差公式证明 郝伟 2020/01/03

[TOC]

1. 简介

在线性回归计算(Linear Regression) 中，有三个非常重要的概念：

• 总离差平方和（Sum of Squares Total） $SST={\sum }_{i=1}^n(y_i-\overline{y}{)}^2$
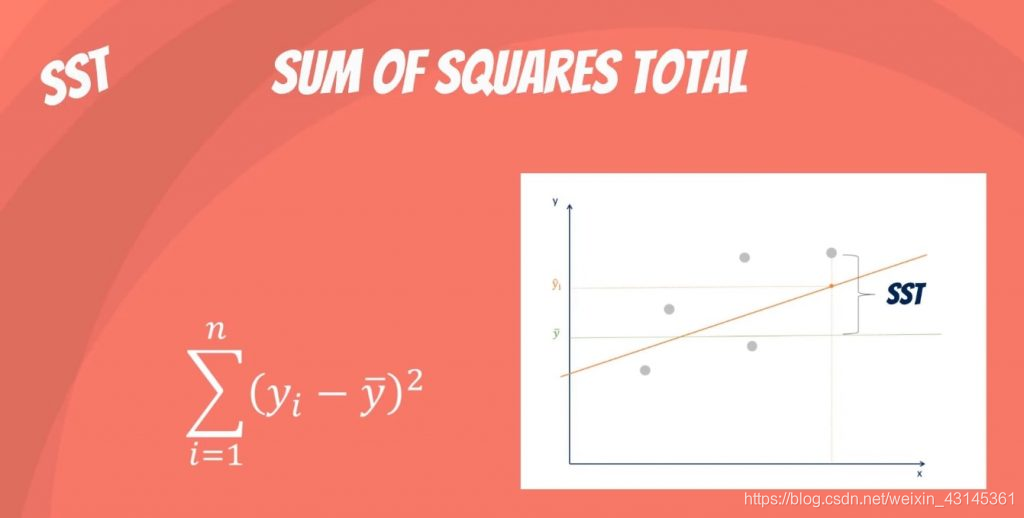
• 残差平方和（Sum of Squared Errors） $SSE={\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2$
• 回归平方和（Sum of Squares Regression ） $SSR={\sum }_{i=1}^n({\hat{y}}_i-\overline{y}{)}^2$

2. 重要关系：SST=SSE+SSR

三者存在下重要关系 $SST=SSE+SSR$

即： ${\sum }_{i=1}^n(y_i-\overline{y}{)}^2={\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2+{\sum }_{i=1}^n({\hat{y}}_i-\overline{y}{)}^2$

这个结论很重要，表明了三者的关系，同时也简化了计算。但是结论似乎很奇怪，因为根据常识，当 $a + b = c$ 成立的时候，$a^2 + b^2 = c^2$ 是不能保证一定成立的。我们将上面的等式展开，化简后可以得到以下等式： $\sum (\widehat{y_i}-\overline{y_i})(y_i-\widehat{y_i})=0$ 所以，我们只要证明这个等式成立，即可证明 $SST = SSE + SSR$，然而发现这个等式还真不好证明，在查阅了大量资料后，总算完成了证明，过程如下所示。

3. 证明

最小二乘回归的基本原理是将误差的平方和最小化。实际上公式中所要求的就是 $e_i=y_i - \hat{y_i}$，我们可以使用微积分找到参数$\beta_0$ 和 $\beta_1$ 的方程式，以使$\sum_0^n e_i^2$ 的值最小。（注：为书写和显示方便直观，在证明过程中省略求和的上下限。)

设 $\hat{y_i} = \beta_0 + \beta_1x_i$，则： $S=\sum _{i=1}^n{e}_i^2=\sum {(y_i-\widehat{y_i})}^2=\sum {(y_i-{\beta }_0-{\beta }_1{x}_i)}^2$

我们的目的就是找到 $\beta_0$ 和 $\beta_1$ 使总和 $S$ 最小的值。根据高等数据的基本原理，一个函数取得最值的点的导数为0。由此可得，$S$ 求相对于 $\beta_0$ 的偏导数为零，即：

$\frac{\partial S}{\partial {\beta }_0}=\sum 2{(y_i-{\beta }_0-{\beta }_1{x}_i)}^1(-1)=0$

化简后得到： $$\sum (y_i-{\beta }_0-{\beta }_1{x}_i)=0$$

即 $$\begin{array}{}\sum (y_i-\widehat{y_i})=0& \text{(Eq.1)}\end{array}$$

然后，再重新排列并求解 $\beta_0$， $\sum {\beta }_0=\sum y_i-{\beta }_1\sum x_i$

$n{\beta }_0=\sum y_i-{\beta }_1\sum x_i$

${\beta }_0=\frac{1}{n}\sum y_i-{\beta }_1\frac{1}{n}\sum x_i$

在求完$\beta_0$的偏导数以后，我们再求 $S$ 相对 $\beta_1$ 的偏导数，同理有： $\frac{\partial S}{\partial {\beta }_1}=\sum 2{(y_i-{\beta }_0-{\beta }_1{x}_i)}^1(-x_i)=0$

等式两边同时除以 $-2$ 再重新排列，可得：

$\sum x_i(y_i-{\beta }_0-{\beta }_1{x}_i)=0$

即 $\sum x_i(y_i-\widehat{y_i})=0$

又因为 $\hat{y_i} = \beta_0 + \beta_1x_i$，所以 $x_i=\frac{1}{{\beta }_1}(\widehat{y_i}-{\beta }_0)=\frac{1}{{\beta }_1}\widehat{y_i}-\frac{{\beta }_0}{{\beta }_1}$

最后，再将其代入上面的方程式，即可得到预期的表达式： $\sum x_i(y_i-\widehat{y_i})=0$

$\sum (\frac{1}{{\beta }_1}\widehat{y_i}-\frac{{\beta }_0}{{\beta }_1})(y_i-\widehat{y_i})=0$

$\frac{1}{{\beta }_1}\sum \widehat{y_i}(y_i-\widehat{y_i})-\frac{{\beta }_0}{{\beta }_1}\sum (y_i-\widehat{y_i})=0$

现在，第二项为零（由 $eqn.1$ 表示），因此，我们立即得到所需的结果： $\begin{array}{}\sum \widehat{y_i}(y_i-\widehat{y_i})=0& \text{(Eq. 2)}\end{array}$

最终，根据 $Eq.2 - \bar y * Eq.1$ 可得 $\sum \widehat{y_i}(y_i-\widehat{y_i})-\overline{y}\sum (y_i-\widehat{y_i})=0$

即 $\sum (\widehat{y_i}-\overline{y_i})(y_i-\widehat{y_i})=0$

综上，我们最终可以得到以下结论： ${\sum }_{i=1}^n(y_i-\overline{y}{)}^2={\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2+{\sum }_{i=1}^n({\hat{y}}_i-\overline{y}{)}^2$

4. 结论

通过以上证明过程，我们证明了 $SST=SSE+SSR$。但是正如前言所说，当 $a + b = c$ 成立的时候，$a^2 + b^2 = c^2$ 是不能保证一定成立的，这里的等式之所以成立，是因为有个重要的前提就是拟合值最小，所以我们才可以用$\frac{\partial{S}}{\partial{\beta_0}} = 0$ 和 $\frac{\partial{S}}{\partial{\beta_1}} =0$ 两式联立进行求解。如果没有这个条件，即拟合过程中没有取得最值，这个结论是不能保证成立的。

5. 参考资料

[1] https://stats.stackexchange.com/questions/207841/why-is-sst-sse-ssr-one-variable-linear-regression/401299#401299 [2] https://math.stackexchange.com/questions/709419/prove-sst-ssessr [3] https://web.njit.edu/~wguo/Math644_2012/Math644_Chapter%201_part4.pdf [4] https://365datascience.com/sum-squares/